De andere helft van de priemgetallen ...
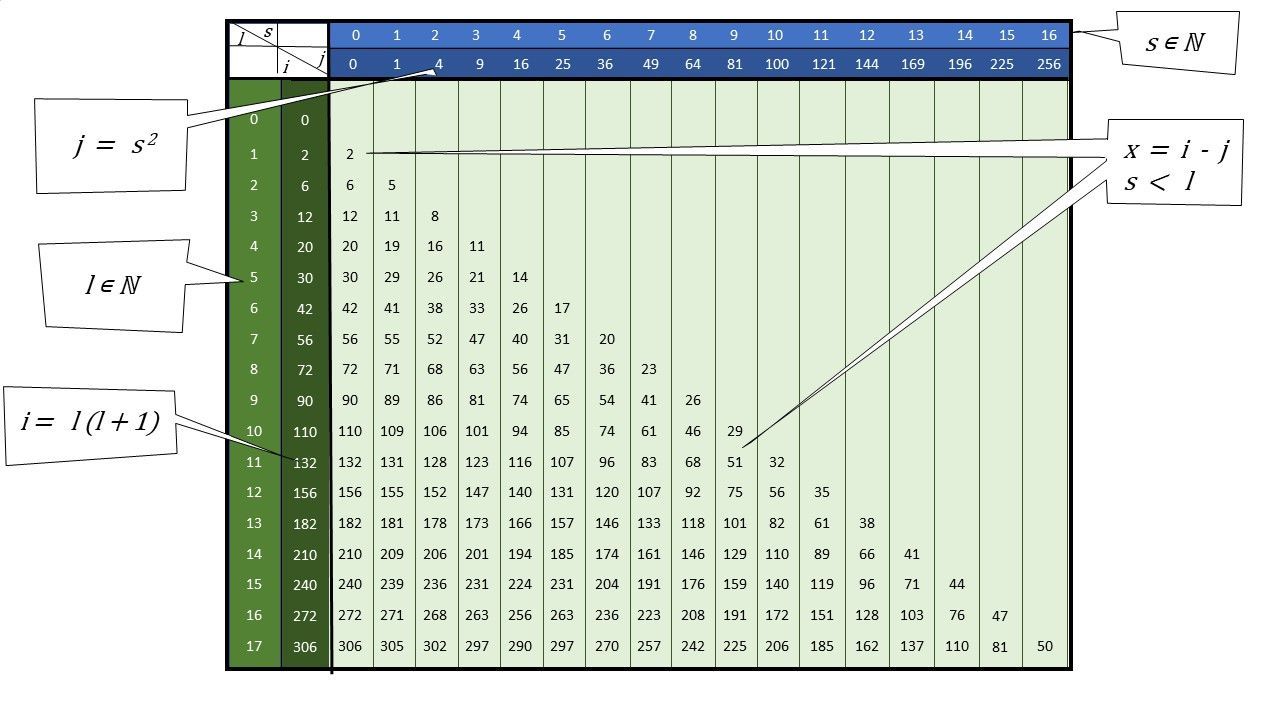
In de eerste kolom staan de natuurlijke getallen netjes onder elkaar. In de tweede kolom staan de kwadraten van de getallen uit de eerste kolom waarbij het getal zelf wordt opgeteld. Zo staat er op de negende rij het getal 90 = 9x9 + 9. Op de bovenste rij staan de natuurlijke getallen netjes naast elkaar. Op de tweede rij staan de kwadraten van de getallen op de eerste rij. Het is duidelijk dat men ook hier de tabel eindeloos groot kan maken. De getallen binnen de tabel worden gevormd door het getal van de tweede rij af te trekken van het getal van de tweede kolom. Zo staat er op de kruising van rij 9 en kolom 4 het getal 74 wat 74 = 90 – 16 is. Wij zorgen er wel voor dat het kolomnummer steeds kleiner is dan het rijnummer. Wij merken dat dit een reeks getallen oplevert waarbij er getallen ontbreken. En zie je dat de diagonalen steeds met stappen van 3,5,7,9,11 … etc. oplopen?

De ontbrekende getallen zijn:
1, 3, 4, 7, 9, 10, 13, 15, 18, 22, 24, 25, 27, 28, 34, 37, 39, …
Men kan deze reeks makkelijk uitbreiden door de tabel groter te maken.
Deze rij kan dus door de volgende formule worden voorgesteld:
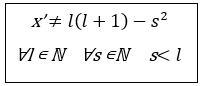
Wanneer wij de getallen in de reeks vermenigvuldigen met 4 en daar vervolgens 1 bij optellen dan bekomen we de nieuwe reeks:
5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …
Deze rij kan door de volgende formule worden voorgesteld:
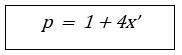
En wat zien we: dit zijn allemaal priemgetallen van de vorm 1 + 4x netjes op een rij !!!!!!!
